Spouses Dilemma -1
*In trying to explain this variant of the Prisoner’s Dilemma – a model that involves strategic decision making, I have tried, not to use vocabulary that requires a degree in Game Theory to understand. However certain words need to be understood in order to appreciate the article. I have explained these terms as and when required in
Consider a one stage game in which John and L simultaneously choose between cleaning the house and loafing on a single day.
Before moving further, a quick look at some definitions and concepts:
Game: A situation in which a number of individuals make decisions and each cares about his own choices and other’s choices.
One stage game: A game in which each player makes all of his choices before observing any choice by the other players.
Infinitely Repeated game: Is formed by playing a one stage game many times in succession.
Strategy: Any rule that specifies a choice based on the history of past choices.
Best Response: A strategy that provides a player with the highest possible payoff, assuming that other players behave in a specified way.
Dominant Strategy: The only best response of a player regardless of other people’s choices.
*Nash Equilibrium: In Nash equilibrium the strategy played by each player in a game is a best response to the strategies played by everybody else. In other words, every player correctly anticipates what everyone will do and then chooses the best possible alternative.
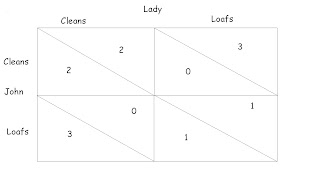
Suppose the following are their payoffs in doing each activity:
According to this table:
Both prefer loafing to cleaning regardless of what the other chooses. If John chooses to clean (upper row), the lady gets a higher payoff of 3 if she loafs rather than if she cleans (upper triangles in upper row). Similarly this holds true for John if the lady chooses to clean (check left column). That is, loafing is the dominant strategy for both the players.
Also if one cleans the house, the other is happier than if neither of them cleans the house. Check the pay-offs in the upper right and lower left squares.
Lastly, both of them would rather have their house clean than dirty. Check the pay-offs in the upper left and lower right squares.
Without repetitions, the only Nash equilibrium for John and his Lady is to loaf (bottom-right square). If the problem of ‘who shall clean the house?’ persists over a period of time, this one stage game turns into a repeated game. The lady can choose from a number of strategies, to resolve this dispute. For example,
• Never Clean
• Always Clean,
• Loaf if John loafed the previous day, otherwise clean
The same applies to John as well. Anyway if both choose to loaf always, that would be the Nash equilibrium, because on any given day, loafing gives a higher pay-off for both of them, and doesn’t affect the future behaviour of the other. This equilibrium involves no cooperation.
To be Continued...
*In 1950, 22- year-old John Nash proposed The Nash Equilibrium for thinking about strategic decisions, for which he later received a Nobel Prize.


Comments
Where did you get this from? Game theory is an important aspect of any AI class!